インフレ・・・物価が二倍になる日はいつか?
今、物価高が問題になっています。総務省統計局によれば、2022年10月の消費者指数は、3.6%(生鮮食料品の除く年率)と発表され、インフレに大きな関心があつまっています。
「このまま、これが続いたらそのうち物価が2倍になっちゃうよ」
「そうだね、んー、それって何年後かな?」
こんな会話が聞こえるとき、ある人は、スマホを取り出し、ある人は、エクセルを立ち上げ・・・・。
不動産鑑定士なら暗算!で「約19年ですね」と、いえるかどうかわかりませんが、じつは、簡単に計算する方法があるのです。

Index
2倍になる年数が暗算できる!
ある数がPパーセントで増えるときに元の数が2倍になる年数は、
N年 = 70 ÷ P
で求めることができます。実に簡単ですね。「インフレ略算法」とここでは勝手に名付けておきます。
本件では、70÷3.6=19.4444≒19年となります。
もっと実生活的にみてみます。いま、100円で売っているコンビニのおにぎりがあったとします。このおにぎりが、インフレで毎年10%(P)づつ値上げしたとします。すると(上の式で計算:70÷10=7)、たった7年で2倍の200円になってしまうと計算できるわけです。本当でしょうか?
本当にあってるの?検証してみましょう
物価上昇率3.6%のとき19年後は本当に2倍になるか計算してみます。
不動産鑑定士的には、複利終価率が2になるか検証することになります。
(1+0.036)^19 ≒ 1.96 ≒ 2.0
それでは10%のときはどうでしょうか。上記式では7年です(コンビニおにぎりの例)。
(1+0.1)^7 ≒ 1.95 ≒ 2.0
面倒な計算をしなくても2倍になる年数=70÷Pは便利ですね。
小難しいことをいうと、下記の複利終価率の式で、終価率(2.0)とr(3.6%)が決まったときにn(年)を求めたのです。
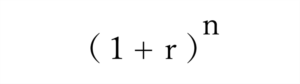
複利終価率の式
インフレ略算法を活用しよう(応用編)
この式の70を以下のとおり入れ替えることで、2割増、3割増、5割増になる年数も簡単に求めることができます。
難しい理屈はぬきにして覚えておきましょう。
20%増加する年数 N年 = 20 ÷ P%、もう少し精度良く求めるには 19 ÷ P%
30%増加する年数 N年 = 30 ÷ P%、もう少し精度良く求めるには 27 ÷ P% ※
50%増加する年数 N年 = 40 ÷ P%、もう少し精度良く求めるには 41 ÷ P%
100%増加する年数 N年= 70 ÷ P%、もう少し精度良く求めるには 73 ÷ P%
これらは、不動産鑑定の実務経験則によるものですが、覚えておくと役に立つのではないかと思います。特に証券化の鑑定評価では必須!です。
※ 数学に興味のある方へ “27”以外は素数であることにご注目ですね。